
5.3 Weitere Möglichkeiten
zur Bestimmung der Varianz- Kovarianz- |
|
||||||||
| > weiter | |||||||||
| [143] Vgl. Bollerslev (1986). [144] Dies trägt dem sogenannten „volatility clustering“ Rechnung. Unter „volatility clustering“ versteht man die empirisch beobachtbare Tendenz, dass Wertpapierpreise nach einem außergewöhnlich starken Anstieg oder Rückgang der Preis meist einige Zeit noch sehr volatil sind. [145] Eine umfangreiche Übersicht über diese Modelle findet sich u.a. in Engle (1993). |
|||||||||
 Nach oben I Home
I Impressum
Nach oben I Home
I Impressum 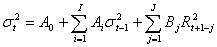 (37)
(37)