 |
5.1 Die Bedeutung der
Varianz- Kovarianz- Matrix in der Asset
Allocation
Die Verwendung historischer Varianzen und Kovarianzen als Schätzer
der
zukünftigen Varianzen kann - im Vergleich mit der Bestimmung
der erwarteten
Rendite- vor allem aus zwei Gründen als deutlich weniger problematisch
angesehen werden: Erstens wirken sich Schätzfehler bei den
Varianzen und
Kovarianzen, wie in Kapitel 3 gezeigt wurde, deutlich schwächer
auf die optimale
Portfolioallokation aus als Schätzfehler bei den erwarteten
Renditen. Zweitens ist
die Größe der Schätzfehler bei einer Schätzung
der zukünftigen Varianzen und
Kovarianzen anhand historischer Werte deutlich geringer als bei
den Renditen.
Dies liegt im Wesentlichen daran, dass - im Gegensatz zur Ermittlung
der
erwarteten Renditen - eine Erhöhung der Datenfrequenz innerhalb
eines
vorgegebenen Zeitraums zur Reduktion des Schätzfehlers führt.137
Die Standardabweichung des Mittelwertes bzw. die Höhe des Schätzfehlers
beträgt bei einer historischen Ermittlung der erwarteten Rendite,
wie bereits in
Abschnitt 4.2.1 gesehen,
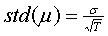 (12) (12)
bzw.
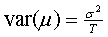 (12`) (12`)
hängt also, im Falle der Renditen, bei gleich bleibendem Beobachtungszeitraum
nicht von der Datenfrequenz ab.
Im Vergleich dazu bestimmt sich die Güte des Schätzers
der Varianz mit
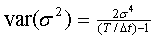 (32) (32)
mit T = n* Δt und n als der Anzahl der Beobachtungszeitpunkte.138
Die Güte des Schätzers der Varianz kann also durch eine
Erhöhung der
Beobachtungszeitpunkte verbessert werden. Je höher die Datenfrequenz,
desto
geringer ist, zumindest theoretisch, die Höhe des Schätzfehlers.
Es ist also
denkbar, durch Verkürzungen der Beobachtungsintervalle, z.B.
auf täglicher,
stündlicher oder sogar minütlicher Basis die Güte
dieses Schätzers immer weiter
zu verbessern. Jedoch stehen dem einige praktische Schwierigkeiten
entgegen.
Eine sehr hohe Datenfrequenz bringt nämlich das Problem mit
sich, dass die
erhobene Datenmenge durch den sogenannten „market noise“
verfälscht wird.
Unter „market noise“ versteht man kleinere Marktbewegungen,
die zufällig
entstehen und oft durch kleine Umsätze hervorgerufen werden.
Auch stellen die
Preisbewegungen über sehr kurze Zeiträume oft einfach
Veränderungen in den
Geld/Brief- Spannen dar. Des weiteren ergeben sich oft signifikante
Veränderungen der Volatilitäten innerhalb kurzer Zeiträume,
z.B. vor oder nach
der Veröffentlichung marktrelevanter Fundamentaldaten. Betrachtet
man sehr
kurze Zeiträume, können die Märkte in diesem Sinne
als nicht mehr effizient
gelten.
Auch bedeutet eine sehr hohe Datenfrequenz, dass die empirisch beobachteten
Renditen nicht mehr unabhängig, identisch und normalverteilt
sind.
Litterman und Winkelmann haben anhand einer Monte- Carlo Simulation
gezeigt,
dass Aktienrenditen bei hohen Datenfrequenzen autokorreliert sind.139
Des
weiteren weisen sie eine Verteilung der Renditen nach, die bei hohen
Datenfrequenzen nicht mehr durch die Normalverteilung approximierbar
ist,
sondern sogenannte „fat tails“ besitzt, d.h. zu viel
Masse an ihren Enden aufweist.
Dennoch ist die historische Bestimmung der Varianzen und der Kovarianzen
mit
deutlich geringeren Schätzfehlern behaftet als bei der Verwendung
historischer
Renditen als Schätzer der ex- ante Renditen.
In der Praxis wird sogar oft aufgrund der Größe der Schätzfehler
in den
Renditegrößen sowie deren starken Einfluss auf die resultierenden
Portfoliogewichte auf die Bestimmung der erwarteten Renditen im
Rahmen der
Mean- Variance Optimierung verzichtet und nur das sogenannte „Minimum-
Varianz“ Portfolio bestimmt. Dabei wird nur eine Schätzung
der Varianz-
Kovarianz- Matrix, meist aus historischen Daten, vorgenommen, während
die
Renditegrößen konstant und gleich gehalten werden.
Im folgenden Abschnitt wird ein Verfahren für die historische
Ermittlung der
Varianz- Kovarianz vorgestellt, um dann trotz der relativ hohen
Güte dieses
Schätzers der einfachen historischen Ermittlung einen kurzen
Überblick über
weitere Verfahren zu geben.
|
 |
| Info |
|
|
|
 |
|

 Nach oben I Home
I Impressum
Nach oben I Home
I Impressum 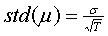 (12)
(12)
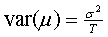 (12`)
(12`)
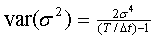 (32)
(32)