 |
4.2.4 Prognosen mittels
Renditeregressionen
Unter der Annahme zeitvariabler Risikoprämien interessiert
weniger die
durchschnittlich realisierte Risikoprämie, sondern vielmehr
die Frage ob die ex-
ante erwarteten Renditen und Risikoprämien zum momentanen Zeitpunkt
ungewöhnlich hoch oder tief sind. Da Preise relativ zu ihren
fundamentalen
Kennzahlen wie Dividenden oder Gewinnen nicht ewig ansteigen können,50
bedeuten hohe Preise auf den Aktienmärkten entweder einen von
den Investoren
erwateten Anstieg dieser Fundamentalkennzahlen und/oder niedrigere
zukünftige
Marktrenditen.51
Die meisten Autoren in der jüngeren Literatur propagieren den
preisbasierten
Ansatz und folgern aus den momentan im historischen Vergleich hohen
Kurs-
Gewinn- (P/E) bzw. Kurs- Dividenden- (P/D) Verhältnissen niedrigere
(und damit
zeitvariable) zukünftige Renditen und Risikoprämien.52
Dem widersprechen
Ibbotson und Chen, die hohe Kurs- Gewinn- Verhältnisse implizit
auf hohe vom
Markt eskomptierte Gewinnwachstumsraten zurückführen.53
Ibbotson und Chen kombinieren dabei die Annahme der Markteffizienz,
die
Annahme konstanter Risikoprämien und die Annahme, dass niedrige
Ausschüttungsraten von Gewinnen hohe zukünftige Wachstumsraten
bedeuten.54
Unter diesen Annahmen kommen sie zu dem Ergebnis, dass die momentan
hohen
Kurs- Gewinn- Verhältnisse die zukünftigen (Überschuss-)
Renditen
nicht beeinflussen.
Die hohen Kurs- Gewinn- Verhältnisse werden dabei also durch
höhere
antizipierte und eskomptierte Wachstumsraten der Gewinne erklärt.
Die
„unsichtbare Hand“ des effizienten Kapitalmarktes sorgt
demnach für
angemessene Preise und kann damit jede fundamentale Bewertungshöhe
und
Ausschüttungsrate erklären.55
Jedoch lassen sich die theoretisch durchaus fundierten Thesen
von Ibbotson
und Chen empirisch nicht bestätigen.
Arnott und Asness zeigen für den Aktienmarkt der USA, dass
niedrige
Ausschüttungsraten entgegen der ökonomischen Intuition
in der Vergangenheit
nicht im Durchschnitt höhere, sondern tiefere Gewinnwachstumsraten
in den
nachfolgenden Perioden zur Folge hatten und zerstören damit
einen Grundstein
der Analyse Ibbotsons und Chens.56
In Abbildung 3 wird dieser Zusammenhang
veranschaulicht:
Abbildung 3: Ausschüttungsraten und
darauffolgende 10- jährige Gewinnwachstumsraten
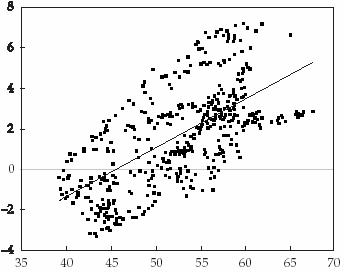
Quelle: Arnott (2001), in: Leibowitz
u.a. (2001), S.86.
Auch findet Asness keine empirische Evidenz, dass hohe P/E- Verhältnisse
in der
Vergangenheit ex- post höhere Wachstumsraten der Gewinne bedeuteten.57
Geht man also davon aus, dass die erwarteten Renditen und Risikoprämien
zeitvariabel sind und sich langfristig den fundamentalen Kennzahlen
angleichen,
ist die Risikoprämie tief, wenn die Preise aus fundamentaler
Sicht hoch sind und
vice versa.
Drobetz hat diese Hypothese durch ein einfaches Regressionsmodell
für die
Schweizer Marktrisikoprämie getestet:58
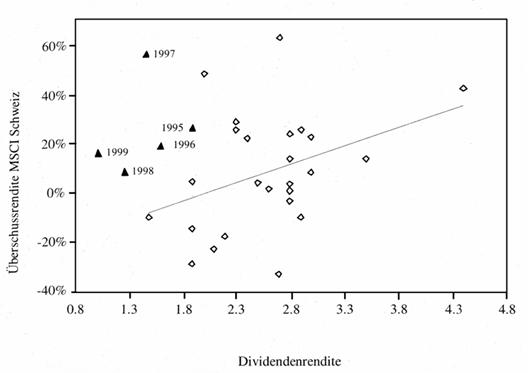
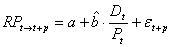 (15)
(15)
wobei RPt->t+p die über p Perioden gemessene
Risikoprämie für die Schweiz im
Zeitraum von 1970-1999 ist.59 Tabelle
3 zeigt das Ergebnis seiner Regression:
Tabelle 3: Regression der Risikoprämie auf die Dividendenrendite
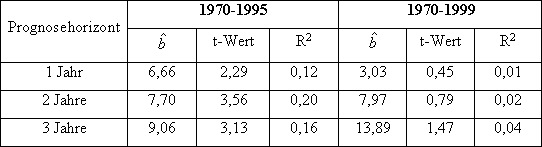
Quelle: Drobetz (2000), S.374.
Der Steigungsparameter 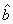 ist für alle betrachteten Zeiträume positiv, was die
ist für alle betrachteten Zeiträume positiv, was die
Annahme niedriger Renditeerwartungen bei (fundamental) hohen Kursen
bestätigt. Im Zeitraum von 1970-1995 liegt der Anteil der erklärten
Varianz R²
der historischen Risikoprämien zwischen 12% und 20%. In diesem
Zeitraum
lassen sich also von fundamentalen Bewertungen Rückschlüsse
auf die
nachfolgenden Risikoprämien ziehen. Da sich die fundamentalen
Bewertungen
im Zeitablauf verändert haben, müssen sich auch die ex-
ante Risikoprämien
verändert haben und damit zeitvariabel sein.
Cochrane berechnet in einer weiteren Studie für den Aktienmarkt
der USA im
Zeitraum von 1947-1996 sogar Erklärungsanteile der Dividendenrendite
auf die
Varianz der nachfolgenden Überschussrenditen R² in Höhe
von 17% (1- jähriger
Prognosehorizont) bis zu 59% (5- jähriger Prognosehorizont).60
Dabei steigt der
Erklärungsgehalt mit dem Prognosehorizont deutlich an. Vor
dem Hintergrund
des viel diskutierten „Random Walk“ der Aktienkurse
erscheint dieser
Erklärungsanteil erstaunlich hoch.61
Jedoch ändern sich Drobetz` Ergebnisse erheblich, wenn man
den Zeitraum von
1995-1999 in die Ergebnisse einbezieht.
Das Bestimmtheitsmaß R² sinkt auf 0% bis 4%, der Steigungsparameter
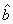
ist mit t-Werten von deutlich unter zwei nicht mehr statistisch
signifikant.
Die fünf Jahre von 1995 bis 1999 vernichten die Erklärungskraft
des
Modells also fast vollständig. Eine Erklärung dafür
kann schnell gefunden werden:
Zum Ende des vergangenen Jahrzehnts stiegen die Preise im Zuge der
Aktienmarkthausse trotz Dividendenrenditen von unter 2% -
entgegen den Schätzungen des Modells - stark an. Abbildung
4 stellt dies grafisch dar:
Abbildung 4: Dividendenrenditen und Überschussrenditen
der Jahre 1970-1999 des MSCI Schweiz
Quelle: Drobetz (2000), S.375.
Jedoch dürfte die seit dem Jahr 2000 anhaltende Aktienmarktbaisse,
die die These
von niedrigen ex- ante Risikoprämien bei hohen Preisen relativ
zu ihren
Fundamentaldaten zu untermauern scheint, die Erklärungskraft
des Modells
zumindest teilweise wieder herstellen. Es ist somit relativ wahrscheinlich,
dass
die ermittelten Daten zwischen 1995-1999 „Ausreißer“
darstellen und damit ein
Indiz für das Vorhandensein einer spekulativen Blase in diesem
Zeitraum sind.
Trevino und Robertson führen in einer jüngeren Studie
ebenfalls für den
Aktienmarkt der USA im Zeitraum von 1949 bis 1997 eine Regression
des Kurs-
Gewinnverhältnisses auf die nachfolgenden Renditen durch.62
Dabei werden die
Ergebnisse Cochranes und Drobetz` qualitativ bestätigt. Der
Anteil der erklärten
Varianz der Renditen R² beträgt dabei je nach Prognosehorizont
7% bis 65%, mit
deutlich ansteigenden Erklärungsanteilen und stark signifikanten
t-Werten für
längere Zeithorizonte.
Die These niedriger (hoher) Renditeerwartungen bei fundamental hohen
(tiefen)
Kursen kann also auch hier bestätigt werden.
Trevino und Robertson gehen dabei noch einen Schritt weiter und
spezifizieren
diese Renditeerwartung in Abhängigkeit des P/E- Verhältnisses.
Sie errechnen
anhand der Regression einen Schätzer für die ex- ante
Rendite des U.S.
Aktienmarktes über einen 5- Jahres Zeitraum. Dabei gehen sie
von einer
jährlichen Renditeerwartung von 20,67% aus, von der dann das
momentane P/E-
Verhältnis, multipliziert mit einem Faktor von 0,57, subtrahiert
wird.
Für ein P/E- Verhältnis von momentan ca. 30 für den
U.S. Aktienmarkt würde
dies eine also eine jährliche Renditeerwatung von 3,57% über
die nächsten fünf
Jahre bedeuten. Für niedrigere P/E- Verhältnisse wäre
dieser Wert entsprechend
höher.
Es ist also davon auszugehen, dass die ex- ante geforderten Renditen
und
Risikoprämien im Zeitablauf variabel waren. Die historisch
realisierten Renditen
und Risikoprämien können jedoch nur gute Schätzer
zukünftiger Renditen und
Risikoprämien darstellen, wenn diese ex- ante- Werte im Zeitablauf
konstant
waren.
Die Verwendung historischer ex- post Renditen und Risikoprämien
als Schätzer
für zukünftige Höhen dieser Werte ist also als äußerst
kritisch zu betrachten.
|
 |
| Info |
|
|
|
 |
|
| |
[50] Vgl. u.a. Campbell/Lo/MacKinlay (1997), S.259.
[51] Vgl. dazu auch die Anmerkungen von Reichenstein anlässlich
einer Diskussion im Rahmen des
Equity Risk Premium Forum, in: Leibowitz u.a. (2001), S.74.
[52] Vgl. z.B. Arnott/ Bernstein (2002), Shiller (2000), oder Siegel
(1999).
[53] Vgl. Ibbotson/Chen (2003).
[54] Vgl. auch Miller/Modigliani (1961).
[55] Die „unsichtbare Hand“ des Marktes geht auf die Idee
von Adam Smith (1776) zurück.
[56] Vgl. Arnott/Asness (2003), S.73ff.
[57] Vgl. Asness (2001), in: Leibowitz u.a. (2001), S.12ff.
[58] Vgl. Drobetz (2000), S.373-375.
[59] Drobetz bestimmt die Risikoprämie als Differenz zwischen
der Rendite des MSCI Total Return
[Index für die Schweiz und des 3- Monats- Euromarktzinssatzes
für Schweizer Franken.
[60] Vgl. Cochrane (1997), S.7-11.
[61] Zu der Thematik des Random Walk vgl. u.a. Malkiel (2000), S.24ff.
|
|

 Nach oben I Home
I Impressum
Nach oben I Home
I Impressum 
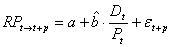 (15)
(15) 
