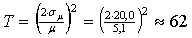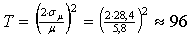|
4.2.1 Historisch erzielte
Renditen und Risikoprämien
Das 20. Jahrhundert kann als das Jahrhundert der Aktie bezeichnet
werden.
Dimson, Marsh und Staunton betrachten den Zeitraum von 1900-2000
in 16
verschiedenen Märkten und zeigen, dass in allen betrachteten
Ländern während
des 20ten Jahrhunderts Aktien eine deutlich höhere durchschnittliche
Rendite
erzielten, als lang laufende Staatsanleihen und kurzfristige Geldmarktanlagen.31
Die Berechnung der jährlichen Durchschnittsrenditen wird dabei
in der Literatur
teils anhand geometrischer und teils anhand arithmetischer Durchschnitte
durchgeführt.32
Bei der Verwendung arithmetischer Durchschnittsrenditen wird implizit
unterstellt, dass der anfangs angelegte Betrag über die Zeit
konstant bleibt. Die
aus der Anlage resultierenden Gewinne werden dabei entnommen, die
Verluste
periodisch ausgeglichen. Arithmetische Durchschnitte werden als
einfacher
Mittelwert der periodischen Renditen berechnet:
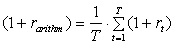 (9)
(9)
Sind die Renditen im Zeitablauf unabhängig und identisch verteilt
(Random-
Walk), stellt das arithmetische Mittel einen statistisch unverzerrten
Schätzer für
die Rendite der Folgeperiode dar. Arithmetische Durchschnittsrenditen
messen
dabei allen möglichen Renditepfaden die gleiche Gewichtung
bei, während
geometrische Durchschnittsrenditen nur den tatsächlich beobachteten
Renditepfad
berücksichtigen.33
Geometrische Renditedurchschnitte sind jedoch zur Bestimmung der
historischen
Performance von Wertpapieren vorzuziehen, da durch sie auch die
Zinsesverzinsung des eingesetzten Kapitals berücksichtigt wird.
Der geometrische
Mittelwert lässt sich wie folgt berechnen:
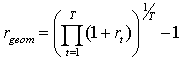 (10) (10)
Die geometrische Durchschnittsrendite kann, unter der Voraussetzung
der
Reinvestition der erzielten Renditen, als Wachstumsrate angesehen
werden, mit
der der angelegte Betrag über den Beobachtungszeitraum wächst.
Bei der Berechnung des erwarteten Endwertes auf Grundlage des arithmetischen
Durchschnittes ist Vorsicht geboten; dieser Wert entspricht zwar
dem erwarteten
Wert des Endvermögens, wird jedoch bei volatilen Wertpapieren
meist aufgrund
einer asymmetrischen Verteilung der Endvermögen unterschritten.
Die
Verwendung arithmetischer Durchschnitte beantwortet somit die Frage,
welche
Rendite man erwarten sollte, wenn zufällig ein einzelnes Jahr
des
Prognosezeitraumes ausgewählt wird. Die geometrische Durchschnittsrendite
hingegen ist bei vorausschauenden Ansätzen derjenige Wert des
Endvermögens,
der mit einer 50%- Wahrscheinlichkeit erreicht wird, sprich der
Median.
Über die korrekte Verwendung dieser Durchschnittswerte für
Prognosen der ex-
ante Risikoprämie besteht in der Literatur durchaus Uneinigkeit.
Wird von einer
unabhängigen und identischen Verteilung der zukünftigen
Renditen ausgegangen,
wird meist der arithmetische Mittelwert vorgezogen, während
unter der Annahme
einer Autokorrelation der Renditen der geometrische Durchschnitt
propagiert
wird.34 Campbell schlägt sogar
die Verwendung eines Mittelwertes aus beiden
Werten vor.35
Grundsätzlich ist dabei der arithmetische Durchschnitt höher
als der
geometrische. Der Unterschied zwischen dem arithmetischen und dem
geometrischen Mittel ist dabei umso größer, je höher
die Volatilität des
betrachteten Renditepfades ist.36
Als Faustformel zur Umrechnung von einem
arithmetischen in einen geometrischen Durchschnitt gilt:
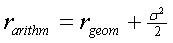 (11)
(11)
Diese gilt als gute Approximation, wenn man logarithmisch normalverteilte
Renditen unterstellt.37
Tabelle 1 zeigt arithmetische und
geometrische jährliche Durchschnitte der realen
Renditen auf Aktien und langfristigen Staatsanleihen sowie die resultierenden
Risikoprämien in den USA, Deutschland, Japan, Frankreich und
Großbritannien
im Zeitraum von 1900-2000.
Tabelle 1: Arithmetisch und geometrisch
erzielte Renditen und Risikoprämien
verschiedener Märkte im Zeitraum von
1900- 2000
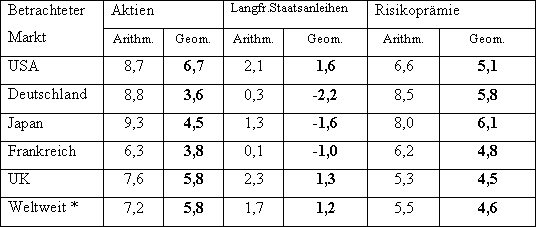
*Weltweit bezieht sich auf den Durchschnitt
der 16 von Dimson/Marsh/Staunton
betrachteten Märkte.
Quelle: Dimson/Marsh/Staunton (2002).
Diese fünf Länder repräsentierten am Anfang des Jahres
2000 zusammen über
75% der weltweiten Marktkapitalisierung in Aktien.38
Im Folgenden werden, wenn nicht anders angegeben, Durchschnittsrenditen
in
geometrischen, realen Werten angegeben.
Die Durchschnittsrendite des Aktienmarktes der USA im Zeitraum von
1900-
2000 betrug 6,7%, mit einer Risikoprämie gegenüber langfristigen
Staatsanleihen
von 5,1%. Deutschland schneidet von den betrachteten Märkten
sowohl bei den
Aktien als auch bei den Anleihen am schwächsten ab. Die durchschnittliche
Rendite von Aktien lag bei 3,6%, die Rendite langlaufender Staatsanleihen
bei
-2,2%, was zu einer Risikoprämie von 5,8% führte. Betrachtet
man für
Deutschland den Zeitraum nach dem Zweiten Weltkrieg von 1950-2000,
erhält
man eine durchschnittliche historische Rendite auf Aktien von 9,1%,
für Anleihen
ergab sich eine jährliche Rendite von 3,7%. Die daraus resultierende
Risikoprämie beträgt 5,4%.
Die jeweiligen Risikoprämien für Japan, Frankreich und
Großbritannien liegen im
Zeitraum von 1900-2000 bei 6,1%, 4,8% und 4,5%.39
In der Praxis werden diese historisch beobachteten ex- post Renditen
häufig als
Schätzer für die ex- ante erwarteten Renditen verwendet.
Dabei wird implizit
unterstellt, dass die beobachteten Renditen im Zeitablauf konstant
sind.
Jedoch ist die historische Betrachtung mit erheblichen Schätzrisiken
belastet.
Tabelle 2 zeigt zusätzlich zu
den beobachteten Durchschnittsrenditen und
Risikoprämien die Volatilität der Renditen von Aktien
und Anleihen für die
Märkte der USA und Deutschlands. Die Größe des Schätzfehlers
wird dabei
durch die Standardabweichung der Mittelwerte gemessen. Von Schätzfehlern
spricht man, wenn die Ausprägungen der zu schätzenden
Parameter von den
tatsächlichen, aber unbeobachtbaren Werten abweichen.
Die Standardabweichung der Mittelwerte bzw. die Höhe des Schätzfehlers
ergibt
sich in Abhängigkeit der Standardabweichung der Rendite und
der Länge des
Untersuchungszeitraums:
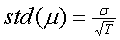 (12)
(12)
Tabelle 2: Historische reale Renditen und Standardabweichungen der
Märkte der USA und Deutschlands im Zeitraum von 1900-2000 (in
%)
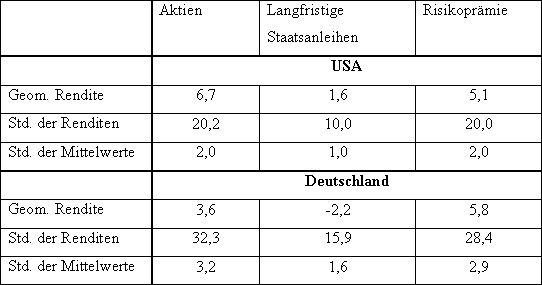
Quelle: Dimson/Marsh/Staunton (2002),
eigene Darstellung.
Auch bei der Verwendung sehr langer historischer Datensätze
verbleibt ein hohes
Schätzrisiko. Für den sehr langen Zeitraum von 1900-2000
ergibt sich, unter der
Annahme einer Normalverteilung der Renditen, in den USA ein 95%
Konfidenzintervall der realen historischen Aktienrenditen zwischen
6,7%-1,96 ·
2,0% = 2,8% und 6,7%+ 1,96 · 2,0% = 10,6%, für Deutschland
ergeben sich auf
Basis des 95% Konfidenzintervalls Werte zwischen 3,6%-1,96 ·
3,2%= -2,7% und
3,6%+1,96 · 3,2% = 9,9%. Die 95% Konfidenzintervalle der
durchschnittlichen
Risikoprämie von Aktien auf langfristige Staatsanleihen liegen
für die USA
zwischen 5,1% -1,96 · 2,0 % = 1,2% und 5% +1,96 ·
2,0% = 8,9% sowie für
Deutschland zwischen 5,8% -1,96 · 2,9% = 0,1% und 5,8% +1,96
· 2,9% =
11,5%.
Durch die hohe Volatilität der historischen Renditen und Risikoprämien
erscheint
es also äußerst schwierig, plausible Aussagen über
die Höhe der zukünftigen
Renditen und Risikoprämien zu treffen.
Immerhin lässt sich eine statistisch signifikante Aussage darüber
treffen, ob die
Risikoprämie auf Aktien langfristig positiv ist. Zwei einfache
t-Tests der Form
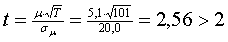 (13)
(13)
für die USA und
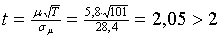 (14)
(14)
für Deutschland zeigen dies auf einem 5% Signifikanzniveau.
Bei gegebenen Parametern ist dafür aber mindestens ein Zeitraum
von rund
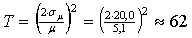
Jahren für die USA und
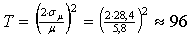
Jahren für Deutschland nötig.
Aufgrund der hohen Schätzunsicherheit werden deshalb in der
Regel sehr lange
Zeiträume betrachtet, um zukünftig erwartete Renditen
und Risikoprämien zu
bestimmen. Jedoch beinhalten diese die Gefahr von Strukturbrüchen;
die
Bedingungen an den Aktienmärkten des 19ten oder frühen
20ten Jahrhunderts
waren grundlegend andere als heute.
|
 |
| Info |
|
|
|
 |
|

 Nach oben I Home
I Impressum
Nach oben I Home
I Impressum 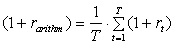 (9)
(9)
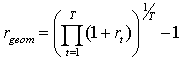 (10)
(10)
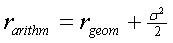 (11)
(11)

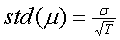 (12)
(12) 
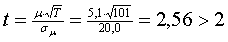 (13)
(13) 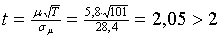 (14)
(14)