6. Das Black- Litterman Modell: Ein Verfahren zur Umsetzung in die
Praxis

Neben den in Kapitel 2 dargestellten Schwierigkeiten bei der praktischen
Umsetzung der klassischen Mean- Variance Optimierung besteht das Problem der
Informationsaggregation. So muss ein Investor, um eine optimale strategische
Portfolioallokation im Sinne der Markowitzschen Portfoliotheorie zu erhalten, für
sämtliche Anlageklassen des Anlageuniversums eine Prognose zur Ermittlung der
zukünftigen Inputparameter abgeben. In einem innovativen Ansatz von Black und
Litterman wird dieses Problem, neben den in Kapitel 2 dargestellten Problemen,
durch die Verwendung von impliziten Gleichgewichtsrenditen umgangen und die
daraus resultierenden optimalen Lösungen intuitiver und in der Praxis besser
umsetzbar gestaltet.146 Black und Litterman verknüpfen dabei die Markowitzsche
Portfoliooptimierung mit den Grundannahmen des CAPM.

Eingang in diese Arbeit findet dieses Modell aufgrund einer möglichen
konsistenten Verknüpfung der in den vorigen Kapiteln geschilderten Verfahren
mit diesen impliziten Gleichgewichtsrenditen, deren Ermittlung auch durchaus als
eigenständige Methode zur Ermittlung der erwarteten Rendite angesehen werden
kann, sowie wegen der Lösung oder zumindest der Minderung der in Kapitel 2
beschriebenen Probleme bei der Umsetzung der klassischen Portfoliotheorie.

Dabei soll der Grundgedanke dieses Modells sowie die Ermittlung der
Gleichgewichtrenditen auf der Grundlage der klassischen Portfoliotheorie relativ
kurz umschrieben werden, für eine anschauliche praktische Umsetzung und eine
ausführliche Beschreibung der formalen Integrierung in den
Portfolioentscheidungsprozess sei auf das Originalpapier sowie die einschlägige
Literatur verwiesen.147
Die Ermittlung der impliziten Gleichgewichtsrenditen erfolgt anhand einer
Umkehroptimierung der Parameter in Gleichung (7). Gegeben sei dabei anstatt
des Vektors der erwarteten Renditen der Vektor der optimalen Portfoliogewichte,
der mit α bezeichnet wird.
Dieser wird von Black und Litterman als Vektor der relativen
Marktkapitalisierungen, also als das Marktportfolio, spezifiziert.
Damit kann dann Gleichung (8`) nach dem Vektor der Überschussrenditen Π
aufgelöst werden. Formal lässt sich dies folgendermaßen darstellen:

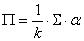(38)

Black und Litterman weisen darauf hin, dass durch die Spezifizierung der
Portfoliogewichte auf das Marktportfolio neutrale Gleichgewichtsrenditen erzeugt
werden, die dem „normalen“ Investitionsverhalten des repräsentativen Investors
entsprechen.148 Unter der Annahme der Kapitalmarkträumung müssen sich
demnach im Gleichgewicht die Renditeerwartungen der Marktteilnehmer so
anpassen, dass das Marktportfolio jenem Portfolio entspricht, welches alle
Investoren auch halten möchten.149 Dabei unterstellen Black und Litterman nicht,
dass sich der Kapitalmarkt jederzeit im Gleichgewicht befindet, sondern
vielmehr, dass Abweichungen der erwarteten Renditen vom Gleichgewicht nicht
dauerhaft auftreten können und damit mittelfristig zu einem gleichgewichtigen
Zustand zurückkehren müssen.
Für die Ermittlung der Varianzen- Kovarianz- Matrix der erwarteten Renditen
schlagen Black und Litterman die Verwendung der historischen Varianz-
Kovarianz- Matrix vor.

Die Gleichgewichtsrenditen stellen dabei einen neutralen Referenzpunkt des
Anlegerportfolios dar, mit dem anschließend die subjektiven Renditeprognosen
des einzelnen Investors verbunden werden.
Obwohl der Grundgedanke des Black/Litterman Modells auf eine Verknüpfung
kurzfristiger Anlagestrategien mit der strategischen Zielsetzung des Investors
abzielt, ist es im Rahmen der strategischen Asset Allocation durchaus denkbar,
neutrale Gleichgewichtsrenditen mit längerfristigen individuellen
Renditeprognosen der einzelnen Anlageklassen zu verbinden und damit
ökonomisch plausiblere und stabilere (Ziel-) Portfoliogewichtungen zu erhalten.

Diese längerfristigen Renditeprognosen können im Rahmen der strategischen
Asset Allocation z.B. durch die im Kapitel 4 vorgestellten Verfahren erfolgen.
Gemäß den subjektiven Renditeprognosen und Markterwartungen des einzelnen
Anlegers kommt es in der konkreten Ausgestaltung des Portfolios zu
Abweichungen von den impliziten Gleichgewichtsrenditen, die umso größer
ausfallen, je höher die Fähigkeiten des Investors zur Ermittlung der zukünftigen
Renditegrößen gehalten werden bzw. je besser die Güte der dem
Prognoseverfahren zugrundeliegenden Modelle geschätzt wird. Es ist dabei
möglich, sowohl Prognosen unter Unsicherheit als auch Prognosen unter
Sicherheit zu integrieren sowie die Prognose relativer und absoluter
Renditeprognosen zuzulassen.

Dabei muss der Investor nur Renditeprognosen für diejenigen Anlageklassen
abgeben, für die er auch tatsächlich eine eigene Meinung besitzt. Das Problem der
traditionellen Mean- Variance Analyse, für jede einzelne Anlageklasse eigene
Prognosen erstellen zu müssen, wird damit umgangen.
Durch die Kombination individueller Renditeprognosen mit impliziten
Renditeerwartungen des Marktes fallen die Veränderungen in den
Portfoliogewichten deutlich geringer aus.150

Daraus resultieren deutlich stabilere und intuitivere Portfoliogewichte,
die die Schwächen des klassischen Mean- Variance Ansatzes bezüglich
extremer Portfolioallokationen und extrem sensitiver Reaktionen auf
Veränderung in den Renditeerwartungen sowie das Problem der Informationsaggregation auf elegante Weise lösen können.