 |

|
 |
 |
4.3.1 Das Standardmodell
Die folgende Darstellung folgt weitgehend den Ausführungen
von Cochrane
sowie dem Originalpapier.68 Die Nutzenfunktion
für jeden möglichen zukünftigen
Konsumpfad eines repräsentativen Investors wird darin mit
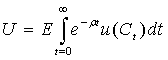 (16) (16)
beschrieben. Ctbezeichnet dabei den Konsum zum Zeitpunkt
t und der Parameter
ρ beschreibt den subjektiven Diskontierungsfaktor
des repräsentativen Investors.
Die Funktion U(·) ist streng monoton steigend und konkav und
beschreibt damit
einen steigenden aber abnehmenden Grenznutzen des Konsums.
Dabei beschreibt u(C) eine Funktion der konstanten relativen Risikoaversion:
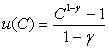 (17) (17)
Der Risikoaversionsparameter γ steht einerseits für die
Höhe der Risikoaversion
und andererseits die Bereitschaft der Investoren, ihren Konsum über
die Zeit zu
substituieren. Die intertemporale Substitutionselastizität
ψ ist dabei direkt mit
dem Risikoaversionsparameter γ verbunden.69
Die Intuition dahinter ist, dass,
wenn Konsumenten abgeneigt gegenüber der Variation verschiedener
Zustände
zu einem bestimmten Zeitpunkt sind, sie auch gegenüber der
Veränderung des
Konsums über die Zeit abgeneigt sind. Für γ = 0 liegt
dabei Risikoneutralität und
eine perfekte Substitution des Konsums im Zeitablauf vor, γ
= 1 steht für u(C) =
ln(C) und bedeutet, dass jede Verdopplung des Konsums einen identischen
zusätzlichen Nutzen stiftet.
Durch einfaches umformen von Gleichung (17) erhält man:
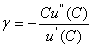 (18) (18)
Hohe γ bedeuten, dass die Investoren eine hohe Risikoaversion
sowie eine
niedrige intertemporale Substitutionselastizität aufweisen.
Dieses Standardmodell dient als Grundlage zahlreicher makroökonomischer
Modelle.70 Auch ist es damit möglich,
die theoretisch von den Investoren
theoretisch benötigte ex- ante Risikoprämie zum Erwerb
risikobehafteter Anlagen
zu ermitteln.
Dabei werden folgende Annahmen getroffen: Die Präferenzen der
Investoren
werden durch die Nutzenfunktion in Gleichung (16) beschrieben, es
besteht ein
vollkommener Kapitalmarkt und es existieren weder Transaktionskosten
noch
Steuern. Die Investoren können dabei eine risikolose und eine
risikobehaftete
Anlage tätigen.
Dabei ergibt sich für die risikolose Anlage ein risikofreier
Zins von:71
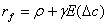 (19) (19)
wobei c die proportionale Veränderung des aggregierten Konsums
beschreibt.
Die Höhe der theoretisch geforderten Risikoprämie beträgt
demnach:
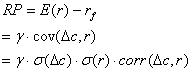 (20) (20)
Gleichung (20) drückt dabei die wohl wichtigste Idee bei der
Bewertung
risikobehafteter Anlagen aus. Sie besagt, dass die Überschussrendite
auf jede
risikobehaftete Anlage proportional zu der Kovarianz dieser Rendite
mit dem
marginalen Nutzen einer zusätzlichen Konsumeinheit und dem
Konsumwachstum
ist.
Die Implikation daraus ist bedeutend: Eine risikobehaftete Anlage
mit der
Standardabweichung σ(r) bietet keine höhere erwartete
Rendite als eine
risikofreie Anlage, wenn sie nicht mit dem Konsumwachstum korreliert
ist. Der
Grund dafür ist die perfekte Diversifizierbarkeit dieser Anlage.
Dies ist auch mit dem CAPM kongruent, das nur für systematische,
nicht
diversifizierbare Risiken höhere erwartete Renditen bestimmt.
Im folgenden Abschnitt wird anhand dieses Modells und plausibler
Inputannahmen versucht, die theoretische von den Investoren geforderte
ex- ante
Risikoprämie abzuleiten. Insbesondere interessant erscheint
dabei ein Vergleich
dieser theoretischen geforderten Risikoprämie mit den tatsächlich
realisierten
historischen Renditen.
|
 |
| Info |
|
|
|
 |
|
| |
|
|
| |
 |
|
| |
[68] Vgl. Cochrane (1997), S.13-16. Cochrane stellt das Modell in
stetiger Zeit dar. Das
Originalpapier ist in diskreter Zeit gehalten und geht auf die Arbeit
von Mehra/Prescott (1985)
zurück. Einen guten Überblick bietet auch Mehra (2003).
[69] Die intertemporale Konsumelastizität ψ ist dabei der
Kehrwert des Parameters γ: ψ = 1/γ.
Vgl. auch Drobetz (2002a), S.19.
[70] Vgl. Cochrane (1997), S.14.
[71] Die formale Herleitung des risikofreien Zinses und der Risikoprämie
findet sich in Cochrane
(1997), S.32-33. |
|
| |
 |
|

 Nach oben I Home
I Impressum
Nach oben I Home
I Impressum 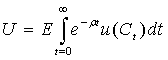 (16)
(16)
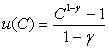 (17)
(17)
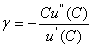 (18)
(18)
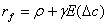 (19)
(19)
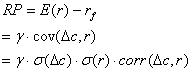 (20)
(20)