3. Relevanz der Inputparameter

Die Mean- Variance Optimierung benötigt die Schätzung der zukünftigen
Renditen, der Varianzen sowie der Kovarianzen. Da über zukünftige
Renditeverteilungen nie vollkommene Sicherheit bestehen kann, ist die Prognose
dieser Inputparameter immer mit Schätzfehlern behaftet. Chopra und Ziemba
haben die Auswirkungen dieser Schätzfehler auf die nach der Mean- Variance
Analyse optimale Portfolioallokation getestet.10 Dabei nahmen sie in einem ersten
Schritt die historischen Renditen von zehn zufällig ausgewählten Werten des Dow
Jones Industrial Average (DJIA) im Zeitraum von 1980-1989 als „wahre“ Werte
der Inputparameter an, um diese dann in einem zweiten Schritt durch einen
Störparameter zu verändern. Mit diesem Störparameter wurde dann in mehreren
Simulationsdurchläufen das daraus resultierende optimale Portfolio bestimmt.
Dabei wurde jeweils einer der drei Parameter verändert, während die anderen
beiden konstant gehalten wurden. Die Veränderung des Nutzens aus diesen durch
den Störparameter veränderten „optimalen“ Portfolios des repräsentativen
Investors wurde von Chopra und Ziemba bei gegebener Risikotoleranz anhand
des Sicherheitsäquivalents angegeben.11

Demnach wirkt sich ein Schätzfehler bei den erwarteten Renditen auf die
optimale Portfolioallokation in der Mean- Variance Analyse ungefähr elfmal so
stark aus wie ein Schätzfehler der Varianzen und ungefähr zwanzigmal so stark
wie ein Schätzfehler der Kovarianzen. Dabei nehmen diese Relationen bei
zunehmender (abnehmender) Risikotoleranz zu (ab). Eine Veränderung in den
Renditeerwartungen um einen Prozentpunkt wirkt sich demnach also ebenso stark
auf die Veränderung der Portfoliogewichte aus wie eine Veränderung um 11% in
den Schätzungen über die zukünftige Varianz.

In einem ähnlichen Ansatz kommen Schäfer und Zimmermann für den deutschen
Aktienmarkt zu vergleichbaren Ergebnissen. Auch sie ermitteln eine vorrangige
Abhängigkeit der aus der Mean- Variance Analyse resultierenden
Portfoliogewichte von der Güte der Schätzung der erwarteten Rendite.12
Diese Ergebnisse werden qualitativ auch von Kempf und Memmel in einer
weiteren Studie bestätigt.13 Sie simulieren dabei für vier Aktien unabhängig
verteilte Wochenrenditen über einen Zeitraum von zwei Jahren. Für jede dieser
Aktien wird dabei eine erwartete Rendite von 11% p.a. und eine
Standardabweichung (Std.) der Renditen von 25% p.a. unterstellt.14 Des weiteren
wird eine Korrelation der Aktien untereinander von 0,3 angenommen.15 Im
Ausgangsportfolio ergibt sich damit eine Gewichtung der Aktien von jeweils
25%. Danach wird unter der Beibehaltung der übrigen Parameter jeweils einer der
Inputparameter bei Aktie 1 um den Wert –10% bis +10% verändert, um das
Ausmaß einer möglichen Fehlschätzung zu bestimmen. Die Ergebnisse von
Kempf und Memmel sind in Abbildung 1 grafisch dargestellt.

Abbildung 1: Auswirkung von Schätzfehlern auf die Höhe der optimalen Portfoliogewichte

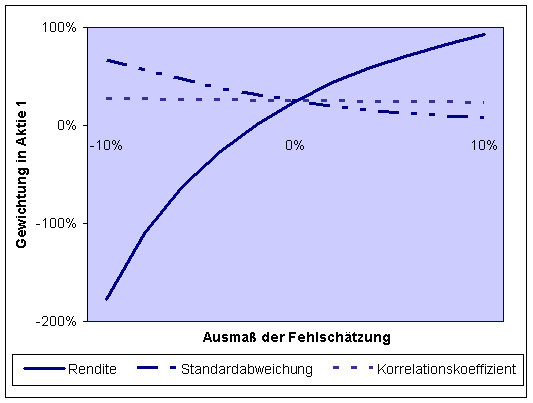
Quelle: Kempf/Memmel (2002), S.900, eigene Darstellung.

Das Sicherheitsäquivalent stellt denjenigen sicheren Betrag dar, aus dem der Investor bei gegebener Risikotoleranz den gleichen Nutzen zieht wie aus dem risikobehafteten Portfolio. Chopra und Ziemba verwenden eine Risikotoleranzhöhe von 50 und geben an, dass die meisten großen institutionellen Anleger eine Risikotoleranz von 40-60 aufweisen dürften.

Es ist deutlich zu erkennen, dass sich Veränderungen hinsichtlich der
Erwartungen über die Höhe der Rendite am stärksten in der
Portfoliozusammensetzung niederschlagen. Von schwächerer Bedeutung ist
demnach die Auswirkung von Schätzfehlern bezüglich der Standardabweichung,
Schätzfehler bezüglich der Korrelationen bzw. Kovarianzen spielen eine deutlich
untergeordnete Rolle in der Ermittlung des Mean- Variance optimierten
Portfolios.

Die Bestimmung der erwarteten Rendite nimmt damit die zentrale Stellung
innerhalb der Mean- Variance Optimierung und der strategischen Asset
Allocation ein.