 |
2. Problemstellung
Die moderne Portfoliotheorie hat ihre Wurzeln in der Mean- Variance
Analyse
von Harry Markowitz. Das darin beschriebene Verhältnis zwischen
der erwarteten
Rendite und des Risikos eines Portfolios hatte weitreichende Auswirkungen
auf
das Portfolio- Management. Auch wenn man sich auch schon vor Markowitz`
Aufsatz der naiven Diversifikation bewusst war,2
lieferte er die mathematischen
Grundlagen, um zu zeigen, dass man durch geschickte Kombination
risikobehafteter Anlagen ein Portfolio erhalten kann, welches aufgrund
des
Diversifikationseffekts bei nicht perfekt korrelierten Anlagen bei
gleicher
Renditeerwartung ein niedrigeres Risiko aufweist.3
Dabei zeigte Markowitz in einer ein- Perioden Betrachtung auf, wie
die
Investoren bei gegebenen Inputparametern ihr Vermögen auf verschiedene
Wertpapiere aufteilen sollten.
Im Folgenden wird ein theoretisches Modell auf der Grundlage von
Markowitz
Arbeit kurz dargestellt um dann auf dessen Schwächen in der
praktischen
Portfolioumsetzung einzugehen.
Angenommen ein Investor hat die Wahl zwischen einem risikolosen
Wertpapier
und einem risikobehafteten Wertpapier, dann ist die Rendite des
Portfolios RP,t+1:
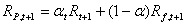 (1) (1)
Dabei bezeichnet α den Portfolioanteil des risikobehafteten
Wertpapiers, R,t+1
bzw. Rf,t+1 sind die Renditen des risikobehafteten bzw.
risikolosen Wertpapiers
vom Zeitpunkt t zum Zeitpunkt t+1.
Die erwartete Rendite dieses Portfolios beträgt dann
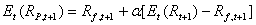 (2)
(2)
mit der Varianz der erwarteten Portfoliorendite von
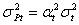 (3) (3)
Die Varianz ist dabei der Parameter, mit dem das Risiko einer Anlage
gemessen
wird. Unter der Annahme eines risikoaversen Investors, der nach
der
Maximierung seiner erwarteten Portfoliorendite unter gleichzeitiger
Minimierung
der Varianz strebt, lässt sich das resultierende Maximierungsproblem
folgendermaßen darstellen:
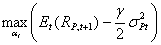 (4) (4)
Dabei beschreibt der Parameter γ die Risikoaversionshöhe
des Investors.
Gleichung (4) lässt sich umschreiben zu:
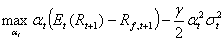 (5) (5)
Als Lösung für dieses Maximierungsproblem erhält
man schließlich
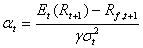 (6) (6)
Der Anteil des risikobehafteten Wertpapiers am Portfolio sollte
also dessen
Überschussrendite oder Risikoprämie auf das risikolose
Wertpapier dividiert
durch das Produkt der Varianz und des Risikoaversionsparameters
entsprechen.
Dieser Ansatz lässt sich problemlos auf den Fall mit mehreren
risikobehafteten
Anlagemöglichkeiten übertragen.4
Diese Anlagemöglichkeiten können im Rahmen der strategischen
Asset
Allocation sowohl verschiedene Anlageklassen als auch im Rahmen
der
taktischen Asset Allocation einzelne Wertpapiere darstellen. Bei
mehreren
betrachteten riskanten Anlagen kann Gleichung (5) umformuliert werden
zu:
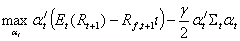 (7)
(7)
Dabei ist Rt+1 nun ein Vektor der riskanten Renditen
mit N Elementen und αt ein
Vektor der Portfoliogewichte der riskanten Anlagen. ∑t
bezeichnet die Varianz-
Kovarianz Matrix der riskanten Renditen, ζ einen Einservektor.
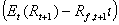 ist
nun der Vektor der Überschussrenditen auf den risikofreien ist
nun der Vektor der Überschussrenditen auf den risikofreien
Zins, die Varianz der Portfoliorendite entspricht 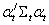 . .
Als Lösung für obiges Maximierungsproblem erhält
man:
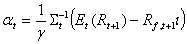 (8)
(8)
Wird dabei 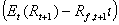 durch Πt ersetzt, lässt sich Gleichung (8)
weiter
durch Πt ersetzt, lässt sich Gleichung (8)
weiter
vereinfachen zu:
  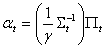 (8`) (8`)
Die Risikoneigung des Investors ist in Gleichung (8`) nur durch
den Skalar 1/ γ
enthalten. Das heißt, dass die Investoren nur Unterschiede
hinsichtlich der
Gewichtung des risikobehafteten Teils innerhalb Portfolios aufweisen,
nicht aber
in der Zusammenstellung dieses risikobehafteten Teils.5
Diese Zusammenstellung hängt lediglich von den Annahmen über
die erwarteten
Renditen der einzelnen Anlagen bzw. Anlageklassen sowie deren Varianzen
und
Kovarianzen ab.
Obwohl die (Standard-) Mean- Variance Analyse ein einperiodisches
Modell
darstellt, lassen sich deren Aussagen gut auf mehrperiodische Modelle
übertragen. So ist es z.B. denkbar, im Rahmen der strategischen
Asset Allocation
eine Mean- Variance Analyse durchzuführen um die einzelnen
Zielgewichtungen
der verschiedenen Anlageklassen zu bestimmen. Im Rahmen der taktischen
Asset
Allocation kann dann mit der Zielsetzung der Performancesteigerung
eine
vorübergehende Abweichung von diesen Zielgewichtungen erfolgen.
Obwohl die Mean- Variance Analyse in der wissenschaftlichen Literatur
eine
herausragende Stellung einnimmt und deren Grundaussagen uneingeschränkte
Akzeptanz finden, ist deren Einfluss auf die praktische Anwendung
immer noch
begrenzt.
Dies liegt hauptsächlich an seiner Sensitivität gegenüber
den getroffenen
Inputannahmen.6 Viele auf Basis plausibler
Inputannahmen erhaltene
Portfoliogewichtungen sind aufgrund daraus resultierender extremer
Portfoliogewichte nicht mit den „intuitiven“ Portfoliovorstellungen
der Investoren
vereinbar. Nach der Mean- Variance Analyse „optimierte“
Portfolios enthalten
häufig extreme Leerverkaufspositionen, welche oft auch aus
rechtlichen und
institutionellen Gründen nicht umgesetzt werden können.7
Bereits aus kleinen
Verschiebungen in den Inputannahmen, die zusätzlich oft große
Schätzunsicherheiten beinhalten, können teilweise starke
Verschiebungen der
Portfoliogewichte resultieren, die häufig ökonomisch nicht
intuitiv und damit von
den Investoren schwer nachvollziehbar sind.8
Aufgrund der Unsicherheit über zukünftige Renditeverteilungen
ist das zentrale
Problem der Mean- Variance Optimierung, dass der Grad der Fundiertheit
des
mathematischen Optimierungsalgorithmus weitaus höher ist als
der Grad der
Information in den Inputparameterschätzungen.
Michaud bezeichnet Investoren, die ihre Portfolios nach der Mean-
Variance
Analyse optimieren, sogar etwas provokativ als „estimation-
error maximizers“.9
Die Stabilität der zu schätzenden Inputparameter ist also
der entscheidende
Grundstein in der Mean- Variance Optimierung. Je besser diese Abschätzung
gelingt, desto fundierter werden die daraus resultierenden optimalen
Gewichte der
einzelnen Anlageinstrumente in der Portfolioallokation sein. |
 |
| Info |
|
|
|
 |
|
| |
[2] Die vor diesem Hintergrund getroffene Aussage „Don't
put all your eggs in just one basket” ist
im angelsächsischen Raum schon sehr lange verbreitet.
[3] Vgl. Markowitz (1952).
[4] Vgl. u.a. Campbell/Viceira (2002), S.20.
[5] Vgl. Tobin (1958).
[6] Vgl. z.B. Drobetz (2002b), Kapitel 1 oder Michaud (1989).
[7] In der Praxis wird daher häufig eine zusätzliche Leerverkaufsrestriktion
formuliert, die jedoch
die Probleme der Mean- Variance Optimierung bestenfalls mindern,
aber nicht lösen kann.
[8] Vgl. Best/Grauer (1991).
[9] Vgl. Michaud (1989), S.33.
|
|

 Nach oben I Home
I Impressum
Nach oben I Home
I Impressum 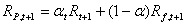 (1)
(1)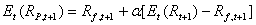 (2)
(2)
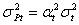 (3)
(3)
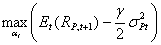 (4)
(4)
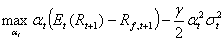 (5)
(5)
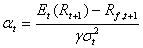 (6)
(6)
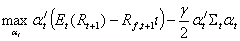 (7)
(7)
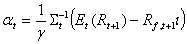 (8)
(8)
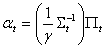 (8`)
(8`)